Bài tập 5 trang 12 toán lớp 11 tập 1 Chân trời:Viết công thức số đo tổng quát của các góc...
Câu hỏi:
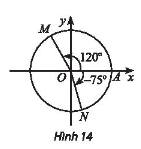
Bài tập 5 trang 12 toán lớp 11 tập 1 Chân trời: Viết công thức số đo tổng quát của các góc lượng giác (OA, OM) và (OA, ON) trong Hình 14
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
Để giải bài toán này, ta cần nhớ lại các công thức cơ bản sau:
1. Góc tam giác lượng giác: Tổng các góc trong một tam giác lượng giác bằng $\pi$ radian.
2. Góc phân giác trong tam giác lượng giác: Góc phân giác của một góc trong tam giác lượng giác bằng nửa góc đó.
3. Góc bù trong tam giác lượng giác: Hai góc bù trong tam giác lượng giác có tổng bằng $\pi$ radian.
Áp dụng các công thức trên vào Hình 14, ta có:
Góc (OA, OM) cho bởi hai góc $\widehat{OAM}$ và $\widehat{MAO}$.
Do $\triangle OAM$ là tam giác lượng giác nên ta có:
$\widehat{OAM} + \widehat{MAO} = \pi$
$\widehat{OAM} = \frac{\pi}{2}$
Vậy góc (OA, OM) là góc phân giác của góc $\widehat{MOB}$, nên $(OA, OM) = \widehat{MOB} = \frac{2\pi}{3} + k.2\pi$ với k là số nguyên.
Tương tự, góc (OA, ON) cho bởi hai góc $\widehat{OAN}$ và $\widehat{NAO}$.
Do $\triangle OAN$ là tam giác lượng giác nên ta có:
$\widehat{OAN} + \widehat{NAO} = \pi$
$\widehat{OAN} = \frac{\pi}{3}$
Vậy góc (OA, ON) là góc bù của góc $\widehat{NOB}$, nên $(OA, ON) = \widehat{NOB} = \frac{5\pi}{12} + k.2\pi$ với k là số nguyên.
Vậy câu trả lời cho câu hỏi là:
$(OA, OM) = \frac{2\pi}{3} + k.2\pi$
$(OA, ON) = \frac{5\pi}{12} + k.2\pi$
1. Góc tam giác lượng giác: Tổng các góc trong một tam giác lượng giác bằng $\pi$ radian.
2. Góc phân giác trong tam giác lượng giác: Góc phân giác của một góc trong tam giác lượng giác bằng nửa góc đó.
3. Góc bù trong tam giác lượng giác: Hai góc bù trong tam giác lượng giác có tổng bằng $\pi$ radian.
Áp dụng các công thức trên vào Hình 14, ta có:
Góc (OA, OM) cho bởi hai góc $\widehat{OAM}$ và $\widehat{MAO}$.
Do $\triangle OAM$ là tam giác lượng giác nên ta có:
$\widehat{OAM} + \widehat{MAO} = \pi$
$\widehat{OAM} = \frac{\pi}{2}$
Vậy góc (OA, OM) là góc phân giác của góc $\widehat{MOB}$, nên $(OA, OM) = \widehat{MOB} = \frac{2\pi}{3} + k.2\pi$ với k là số nguyên.
Tương tự, góc (OA, ON) cho bởi hai góc $\widehat{OAN}$ và $\widehat{NAO}$.
Do $\triangle OAN$ là tam giác lượng giác nên ta có:
$\widehat{OAN} + \widehat{NAO} = \pi$
$\widehat{OAN} = \frac{\pi}{3}$
Vậy góc (OA, ON) là góc bù của góc $\widehat{NOB}$, nên $(OA, ON) = \widehat{NOB} = \frac{5\pi}{12} + k.2\pi$ với k là số nguyên.
Vậy câu trả lời cho câu hỏi là:
$(OA, OM) = \frac{2\pi}{3} + k.2\pi$
$(OA, ON) = \frac{5\pi}{12} + k.2\pi$
Câu hỏi liên quan:
- Câu hỏi mở đầuMỗi hình dưới đây thể hiện chuyển động quay của một điểm trên bánh lái tàu từ vị trí...
- 1. Góc lượng giácKhám phá 1 trang 7 toán lớp 11 Chân trời: Một chiếc bánh lái tàu có thể quay theo...
- Thực hành 1 trang 9 toán lớp 11 Chân trời:Cho $\widehat{MON}$ = $60^{o}$. Xác định số đo của...
- Vận dụng 1 trang 9 toán lớp 11 Chân trời:Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15...
- Hệ thức Chasles (Sa-lơ)Khám phá 2 trang 9 toán lớp 11 Chân trời: Cho Hình 7.a) Xác định số đo các...
- Vận dụng 2 trang 9 toán lớp 11 Chân trời:Trong Hình 8, chiếc quạt có 3 cánh được phân bố đều...
- 2. Đơn vị radianKhám phá 3 trang 10 toán lớp 11 Chân trời:Vẽ đường tròn tâmObán...
- Thực hành 2 trang 10 toán lớp 11 Chân trời:Hoàn thành bảng chuyển đổi đơn vị đo của các góc...
- 3. Đường tròn lượng giácKhám phá 4 trang 11 toán lớp 11 Chân trời: Trong mặt phẳng toạ độ Oxy, vẽ...
- Thực hành 3 trang 12 toán lớp 11 Chân trời:Biểu diễn trên đường tròn lượng giác các góc lượng...
- BÀI TẬPBài tập 1 trang 12 toán lớp 11 tập 1 Chân trời:Đổi số đo của các góc sau đây sang...
- Bài tập 2 trang 12 toán lớp 11 tập 1 Chân trời: Đổi số đo của các góc sau đây sang độ:a) $\frac{\pi...
- Bài tập 3 trang 12 toán lớp 11 tập 1 Chân trời:Biểu diễn các góc lượng giác sau trên đường...
- Bài tập 4 trang 12 toán lớp 11 tập 1 Chân trời:Góc lượng giác $\frac{31\pi }{7}$ có cùng điểm...
- Bài tập 6 trang 12 toán lớp 11 tập 1 Chân trời:Viết công thức số đo tổng quát của góc lượng...
- Bài tập 7 trang 13 toán lớp 11 tập 1 Chân trời:Trên đường tròn lượng giác, hãy biểu diễn các...
- Bài tập 8 trang 13 toán lớp 11 tập 1 Chân trời:Vị trí các điểm B, C, D trên cánh quạt động cơ...
- Bài tập 9 trang 13 toán lớp 11 tập 1 Chân trời:Hải li là một đơn vị chiều dài hàng hải, được...
Bình luận (0)





