Bài tập 2.7.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y với (x;...
Câu hỏi:
Bài tập 2.7. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền nghiệm của hệ bất phương trình 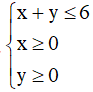
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đạt
Để giải bài toán này, ta cần thực hiện các bước sau:
1. Xác định miền nghiệm của hệ bất phương trình đã cho. Trong trường hợp này, miền nghiệm là miền tam giác có các đỉnh A(6; 0), B(0; 6) và O(0; 0).
2. Tính giá trị của biểu thức F(x; y) = 2x + 3y tại các đỉnh của tam giác AOB:
- F(6; 0) = 2*6 + 3*0 = 12
- F(0; 0) = 2*0 + 3*0 = 0
- F(0; 6) = 2*0 + 3*6 = 18
3. So sánh các giá trị tính được, ta có giá trị lớn nhất là F(0; 6) = 18 và giá trị nhỏ nhất là F(0; 0) = 0.
Vậy, giá trị lớn nhất của biểu thức F(x; y) trên miền nghiệm của hệ bất phương trình là 18 và giá trị nhỏ nhất là 0.
1. Xác định miền nghiệm của hệ bất phương trình đã cho. Trong trường hợp này, miền nghiệm là miền tam giác có các đỉnh A(6; 0), B(0; 6) và O(0; 0).
2. Tính giá trị của biểu thức F(x; y) = 2x + 3y tại các đỉnh của tam giác AOB:
- F(6; 0) = 2*6 + 3*0 = 12
- F(0; 0) = 2*0 + 3*0 = 0
- F(0; 6) = 2*0 + 3*6 = 18
3. So sánh các giá trị tính được, ta có giá trị lớn nhất là F(0; 6) = 18 và giá trị nhỏ nhất là F(0; 0) = 0.
Vậy, giá trị lớn nhất của biểu thức F(x; y) trên miền nghiệm của hệ bất phương trình là 18 và giá trị nhỏ nhất là 0.
Câu hỏi liên quan:
Bình luận (0)





