Bài 9 trang 87 toán lớp 7 tập 1 CTSTQua điểm O, là chốt xoay của một cái kéo, kẻ hai đường thẳng...
Câu hỏi:
Bài 9 trang 87 toán lớp 7 tập 1 CTST
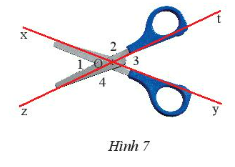
Qua điểm O, là chốt xoay của một cái kéo, kẻ hai đường thẳng xOy và zOt lần lượt song song với hai lưỡi kéo (Hình 7). Tìm các góc kề bù với các góc đối đỉnh có trong hình vẽ.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Giang
Để giải bài toán trên, ta sẽ thực hiện các bước sau:
Bước 1: Vẽ hình theo mô tả trong đề bài.
Bước 2: Gọi $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$ lần lượt là các góc trong hình.
Bước 3: Áp dụng tính chất của các góc đối ở chính giữa và góc kề bù, ta có:
- $\widehat{O_1} = \widehat{O_3}$ (hai góc đối đỉnh)
- $\widehat{O_2} = \widehat{O_4}$ (hai góc đối đỉnh)
- $\widehat{O_1} + \widehat{O_2} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_2} + \widehat{O_3} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_3} + \widehat{O_4} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_4} + \widehat{O_1} = 180^\circ$ (hai góc kề bù)
Bước 4: Giải hệ phương trình để tìm các góc $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$.
Bước 5: Kiểm tra và đưa ra kết luận.
Ví dụ câu trả lời:
Bước 1: Vẽ hình theo mô tả trong đề bài.
Bước 2: Gọi $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$ lần lượt là các góc trong hình.
Bước 3: Ta có:
- $\widehat{O_1} = \widehat{O_3}$
- $\widehat{O_2} = \widehat{O_4}$
- $\widehat{O_1} + \widehat{O_2} = 180^\circ$
- $\widehat{O_2} + \widehat{O_3} = 180^\circ$
- $\widehat{O_3} + \widehat{O_4} = 180^\circ$
- $\widehat{O_4} + \widehat{O_1} = 180^\circ$
Bước 4: Giải hệ phương trình ta được $\widehat{O_1} = \widehat{O_3} = \widehat{O_2} = \widehat{O_4} = 90^\circ$.
Bước 5: Vậy các góc kề bù với các góc đối đỉnh trong hình vẽ là $90^\circ$.
Bước 1: Vẽ hình theo mô tả trong đề bài.
Bước 2: Gọi $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$ lần lượt là các góc trong hình.
Bước 3: Áp dụng tính chất của các góc đối ở chính giữa và góc kề bù, ta có:
- $\widehat{O_1} = \widehat{O_3}$ (hai góc đối đỉnh)
- $\widehat{O_2} = \widehat{O_4}$ (hai góc đối đỉnh)
- $\widehat{O_1} + \widehat{O_2} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_2} + \widehat{O_3} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_3} + \widehat{O_4} = 180^\circ$ (hai góc kề bù)
- $\widehat{O_4} + \widehat{O_1} = 180^\circ$ (hai góc kề bù)
Bước 4: Giải hệ phương trình để tìm các góc $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$.
Bước 5: Kiểm tra và đưa ra kết luận.
Ví dụ câu trả lời:
Bước 1: Vẽ hình theo mô tả trong đề bài.
Bước 2: Gọi $\widehat{O_1}$, $\widehat{O_2}$, $\widehat{O_3}$, $\widehat{O_4}$ lần lượt là các góc trong hình.
Bước 3: Ta có:
- $\widehat{O_1} = \widehat{O_3}$
- $\widehat{O_2} = \widehat{O_4}$
- $\widehat{O_1} + \widehat{O_2} = 180^\circ$
- $\widehat{O_2} + \widehat{O_3} = 180^\circ$
- $\widehat{O_3} + \widehat{O_4} = 180^\circ$
- $\widehat{O_4} + \widehat{O_1} = 180^\circ$
Bước 4: Giải hệ phương trình ta được $\widehat{O_1} = \widehat{O_3} = \widehat{O_2} = \widehat{O_4} = 90^\circ$.
Bước 5: Vậy các góc kề bù với các góc đối đỉnh trong hình vẽ là $90^\circ$.
Câu hỏi liên quan:
- Bài 4 trang 87 toán lớp 7 tập 1 CTSTQuan sát Hình3a) Tính$\widehat{{{B}_{1}}}$b) Chứng...
- Bài 5 trang 87 toán lớp 7 tập 1 CTSTQuan sát Hình 4.Chứng minh rằng:a) AB//CD và EF // CDb) AB //...
- Bài 6 trang 87 toán lớp 7 tập 1 CTSTCho hình 5 có$\widehat{{{B}_{1}}}$ = 130o. Số đo...
- Bài 7 trang 87 toán lớp 7 tập 1 CTSTCho hình 6, biết hai đường thẳng a và b song song với nhau và...
- Bài 8 trang 87 toán lớp 7 tập 1 CTSTVẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d...
Bình luận (0)





