Bài 3 trang 99 toán lớp 7 tập 1 CDỞ Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó...
Câu hỏi:
Bài 3 trang 99 toán lớp 7 tập 1 CD
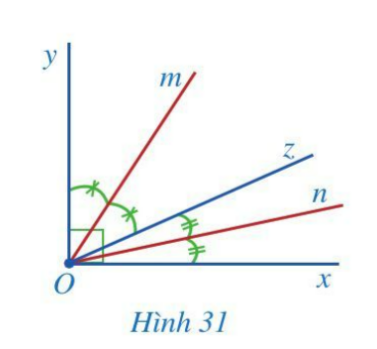
Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và $\widehat{xOn}=\widehat{nOz},\widehat{yOm}=\widehat{mOz}$
a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?
b) Cho biết số đo góc mOn.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Việt
Để giải bài tập trên, ta có thể thực hiện theo các bước sau:a) Ta cần chứng minh rằng các tia Om, On tương ứng là tia phân giác của góc yOz và xOz. - Ta có $\widehat{yOm} = \widehat{mOz}$ và $\widehat{xOn} = \widehat{nOz}$ theo điều kiện đề bài. - Đồng thời, tia Om nằm trong góc yOz và tia On nằm trong góc xOz. - Do đó, ta có thể kết luận rằng các tia Om, On tương ứng là tia phân giác của góc yOz và xOz.b) Để tính số đo góc mOn, ta cần sử dụng tính chất của góc phân giác. - Theo phần a), ta đã chứng minh được rằng $\widehat{yOm}=\widehat{mOz}=\frac{1}{2}\widehat{yOz}$ và $\widehat{xOn}=\widehat{nOz}=\frac{1}{2}\widehat{xOz}$. - Ta biết rằng $\widehat{yOz}+\widehat{xOz}=\widehat{xOy}=90^{\circ}$ vì Oz nằm trong góc xOy. - Từ đó, suy ra $\widehat{mOz}+\widehat{zOn}= \frac{1}{2}\widehat{yOz} + \frac{1}{2}\widehat{xOz} = \frac{1}{2}\widehat{xOy}$ - Vì Oz nằm trong góc mOn, nên $\widehat{mOz} + \widehat{zOn} = \widehat{mOn}$. - Do đó, $\widehat{mOn} = \frac{1}{2} \times 90^{\circ} = 45^{\circ}$.Dưới đây là câu trả lời chi tiết:a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì tia Om nằm trong góc yOz và $\widehat{yOm} = \widehat{mOz}$, tia On nằm trong góc xOz và $\widehat{xOn} = \widehat{nOz}$.b) Góc mOn có số đo là 45 độ.
Câu hỏi liên quan:
{ "content1": "a) Có, tia Om là tia phân giác của góc yOz và tia On là tia phân giác của góc xOz.", "content2": "b) Gọi góc mOn là a. Ta có $\widehat{yOm}+\widehat{mOn}=\widehat{yOz}$ và $\widehat{xOn}=\widehat{nOz}$. Suy ra a = $\frac{1}{2}(\widehat{yOz}-\widehat{xOn})$.", "content3": "Với thông tin $\widehat{xOn}=\widehat{nOz},\widehat{yOm}=\widehat{mOz}$ và $\widehat{yOm}+\widehat{mOn}=\widehat{yOz}$, ta có thể suy luận được rằng tia Om và tia On là tia phân giác của góc xOz và yOz.", "content4": "Để tính số đo góc mOn, ta thực hiện phép tính $\widehat{yOz}-\widehat{xOn}$ và chia kết quả cho 2, ta sẽ có số đo của góc mOn.", "content5": "Trong trường hợp này, số đo của góc mOn sẽ là $\frac{1}{2}(\widehat{yOz}-\widehat{xOn})$."}