4. Định lí Thalès trong không gianKhám phá 5 trang 116 toán lớp 11 tập 1 Chân trời:Cho ba mặt...
Câu hỏi:
4. Định lí Thalès trong không gian
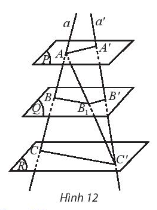
Khám phá 5 trang 116 toán lớp 11 tập 1 Chân trời: Cho ba mặt phẳng song song (P), (Q), (R) lần lượt cắt hai đường thẳng a và a' tại các điểm A, B, C và A', B', C'. Gọi $B_{1}$ là giao điểm của AC' với (Q) (Hình 12)
a) Trong tam giác ACC', có nhận xét gì về mối liên hệ giữa $\frac{AB}{BC}$ và $\frac{AB_{1}}{B_{1}C'}$
b) Trong tam giác AA'C', có nhận xét gì về mối liên hệ giữa $\frac{AB_{1}}{B_{1}C}$ và $\frac{A'B'}{B'C'}$
c) Từ đó,nêu nhận xét về mối liên hệ giữa các tỉ số $\frac{AB}{A'B'},\frac{BC}{B'C'},\frac{AC}{A'C'}$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hưng
Để giải câu hỏi trên, ta có thể sử dụng phương pháp chứng minh đồng dạng của các tam giác.
Đầu tiên, ta chứng minh $BB_{1}//CC'$ trong tam giác ACC':
Gọi I là giao điểm của AC' và B'C.
Áp dụng định lí Thalès trong tam giác AA'C' ta có:
$\frac{AC}{A'C'}=\frac{BC}{B'C}=\frac{BC}{IB'}$
Áp dụng định lí Thalès trong tam giác AB'C ta có:
$\frac{AC'}{A'C'}=\frac{BC'}{B'C'}=\frac{BC'}{IB'}$
Do đó, ta có $\frac{IB'}{B'C}=\frac{BC'}{B'C'}$, suy ra B', I, C' thẳng hàng.
Từ đó, ta có $BB_{1}//CC'$.
a) Trong tam giác ACC', do $BB_{1}//CC'$ nên theo định lí Thalès, ta có:
$\frac{AB}{BC}=\frac{AB_{1}}{B_{1}C'}$
b) Trong tam giác AA'C', ta cũng có $B'B_{1}//AA'$, suy ra theo định lí Thalès:
$\frac{AB_{1}}{B_{1}C}=\frac{A'B'}{B'C'}$
c) Từ a) và b) suy ra:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$
Vậy mối liên hệ giữa các tỉ số đã được chứng minh.
Đầu tiên, ta chứng minh $BB_{1}//CC'$ trong tam giác ACC':
Gọi I là giao điểm của AC' và B'C.
Áp dụng định lí Thalès trong tam giác AA'C' ta có:
$\frac{AC}{A'C'}=\frac{BC}{B'C}=\frac{BC}{IB'}$
Áp dụng định lí Thalès trong tam giác AB'C ta có:
$\frac{AC'}{A'C'}=\frac{BC'}{B'C'}=\frac{BC'}{IB'}$
Do đó, ta có $\frac{IB'}{B'C}=\frac{BC'}{B'C'}$, suy ra B', I, C' thẳng hàng.
Từ đó, ta có $BB_{1}//CC'$.
a) Trong tam giác ACC', do $BB_{1}//CC'$ nên theo định lí Thalès, ta có:
$\frac{AB}{BC}=\frac{AB_{1}}{B_{1}C'}$
b) Trong tam giác AA'C', ta cũng có $B'B_{1}//AA'$, suy ra theo định lí Thalès:
$\frac{AB_{1}}{B_{1}C}=\frac{A'B'}{B'C'}$
c) Từ a) và b) suy ra:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$
Vậy mối liên hệ giữa các tỉ số đã được chứng minh.
Câu hỏi liên quan:
- Câu hỏi mở đầuBề mặt trên của mỗi bậc thang này được đặt như thế nào so với mặt đất?
- 1. Hai mặt phẳng song songKhám phá 1 trang 113 toán lớp 11 tập 1 Chân trời:Hộp giấy có các...
- Vận dụng 1 trang 114 toán lớp 11 tập 1 Chân trời:Tìm một số mặt phẳng song song có trong hình...
- 2. Điều kiện để hai mặt phẳng song songKhám phá 2 trang 114 toán lớp 11 tập 1 Chân trời:Cho...
- Thực hành 1 trang 115 toán lớp 11 tập 1 Chân trời:Cho tứ diện ABCD có E, F, H lần lượt là...
- 3. Tính chất của hai mặt phẳng song songKhám phá 3 trang 115 toán lớp 11 tập 1 Chân trời:a)...
- Khám phá 4 trang 115 toán lớp 11 tập 1 Chân trời:Cho ba mặt phẳng (P), (Q), (R) thoả mãn...
- Thực hành 2 trang 116 toán lớp 11 tập 1 Chân trời:Cho hình chóp S.ABCD có đáy ABCD là hình...
- Vận dụng 2 trang 116 toán lớp 11 tập 1 Chân trời:Khi dùng dao cắt các lớp bánh (Hình 11), giả...
- Thực hành 3 trang 117 toán lớp 11 tập 1 Chân trời:Cho hình chóp S.ABC có SA =9, SB = 12, SC =...
- 5. Hình lăng trụ và hình hộpKhám phá 6 trang 117 toán lớp 11 tập 1 Chân trời:Hình dạng của...
- Khám phá 7 trang 118 toán lớp 11 tập 1 Chân trời:Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD...
- Thực hành 4 trang 119 toán lớp 11 tập 1 Chân trời:Cho hình hộp ABCD.A'B'C'D' và một mặt phẳng...
- Vận dụng 3 trang 119 toán lớp 11 tập 1 Chân trời:Tìm hình lăng trụ có thể lấy một mặt bất kì...
- Bài tậpBài tập 1 trang 119 toán lớp 11 tập 1 Chân trời:Trong mặt phẳng (P) cho hình bình hành...
- Bài tập 2 trang 120 toán lớp 11 tập 1 Chân trời:Cho hình chóp S.ABCD, đáy ABCD là hình bình...
- Bài tập 3 trang 120 toán lớp 11 tập 1 Chân trời:Cho hai hình vuông ABCD và ABEF ở hai mặt...
- Bài tập 4 trang 120 toán lớp 11 tập 1 Chân trời:Cho hình hộp ABCD.A'B'C'D'. Gọi $G_{1}$ và...
- Bài tập 5 trang 120 toán lớp 11 tập 1 Chân trời: Để làm một khung lồng đèn kéo quân hình lăng trụ...
- Bài tập 6 trang 120 toán lớp 11 tập 1 Chân trời:Chỉ ra các mặt phẳng song song trong mỗi hình...
Bình luận (0)





