2. BÁN KÍNH QUA TIÊU VÀ TÂM SAI CỦA PARABOLHoạt động khám phá 2:Cho điểm M(x; y) trên parabol...
Câu hỏi:
2. BÁN KÍNH QUA TIÊU VÀ TÂM SAI CỦA PARABOL
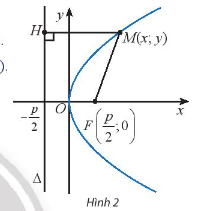
Hoạt động khám phá 2: Cho điểm M(x; y) trên parabol (P): $y^2^ = 2px (H2). Tính khoảng cách từ điểm M đến tiêu điểm F của (P).
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đức
Phương pháp giải:
Ta biết rằng tiêu điểm F của parabol là F(-p, 0).
Gọi A là tâm sai của parabol, ta có A(p, 0).
Khoảng cách từ điểm M(x, y) đến tiêu điểm F có thể tính bằng định nghĩa khoảng cách giữa hai điểm trên mặt phẳng:
MF = √((x + p - (-p))^2 + (y - 0)^2)
= √((x + 2p)^2 + y^2)
= √(x^2 + 4px + 4p^2 + y^2)
Do đó, khoảng cách từ điểm M đến tiêu điểm F của parabol là MF = √(x^2 + 4px + 4p^2 + y^2).
Nhưng với parabol (P): y^2 = 2px, ta thay y^2 = 2px vào công thức trên, ta được:
MF = √(x^2 + 4px + 4p^2 + 2px)
= √(x^2 + 6px + 4p^2)
Vậy, khoảng cách từ điểm M(x, y) trên parabol đến tiêu điểm F của parabol là: MF = √(x^2 + 6px + 4p^2).
Ta biết rằng tiêu điểm F của parabol là F(-p, 0).
Gọi A là tâm sai của parabol, ta có A(p, 0).
Khoảng cách từ điểm M(x, y) đến tiêu điểm F có thể tính bằng định nghĩa khoảng cách giữa hai điểm trên mặt phẳng:
MF = √((x + p - (-p))^2 + (y - 0)^2)
= √((x + 2p)^2 + y^2)
= √(x^2 + 4px + 4p^2 + y^2)
Do đó, khoảng cách từ điểm M đến tiêu điểm F của parabol là MF = √(x^2 + 4px + 4p^2 + y^2).
Nhưng với parabol (P): y^2 = 2px, ta thay y^2 = 2px vào công thức trên, ta được:
MF = √(x^2 + 4px + 4p^2 + 2px)
= √(x^2 + 6px + 4p^2)
Vậy, khoảng cách từ điểm M(x, y) trên parabol đến tiêu điểm F của parabol là: MF = √(x^2 + 6px + 4p^2).
Câu hỏi liên quan:
- 1. TÍNH ĐỐI XỨNG CỦA ĐƯỜNG PARABOLHoạt động khám phá 1: Chứng tỏ rằng nếu điểm M(x0; y0) nằm trên...
- Thực hành 1: Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các...
- Vận dụng 1: Trong mặt phẳng xoy, cho điểm A(2,0) và đường thẳng d: x+2=0. Viết phương trình của...
- Thực hành 2: Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng:a,Điểm M1(1; –4)...
- Vận dụng 2: Một cổng có dạng một đường parabol(P).Biết chiều cao của cổng là 7,6 m và khoảng...
- Vận dụng 3:Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc...
- BÀI TẬP1.Tìm tọa độ tiêu điểm và phương trình đường chuẩn của các parabol sau:a,(P1):...
- 2.Tính bán kínhtrênqua tiêu của điểm đã cho trên các parabol sau:a) Điểm M1(3;...
- 3.Trong mặt phẳng Oxy, cho điểm A($\frac{1}{4}$; 0)và đường thẳng d: x+ $\frac{1}{4}$ =...
- 4.Cho parabol (P). Trên (P) lấy hai điểm M, N sao cho đoạn thẳng MN đi qua tiêu điềm F của...
- 5. Hãy so sánh bán kính qua tiêu của điểm M trên parabol (P) với bán kính của đường tròn tâm M,...
- 6.Một sao chổi A chuyển động theo quỹ đạo có dạng một parabol (P) nhận tâm Mặt Trời là tiêu...
- 7.Mặt cắt của gương phản chiếu của một đèn pha có dạng một parabol (P) có phương trình chính...
Bình luận (0)





